Cyrus Samii

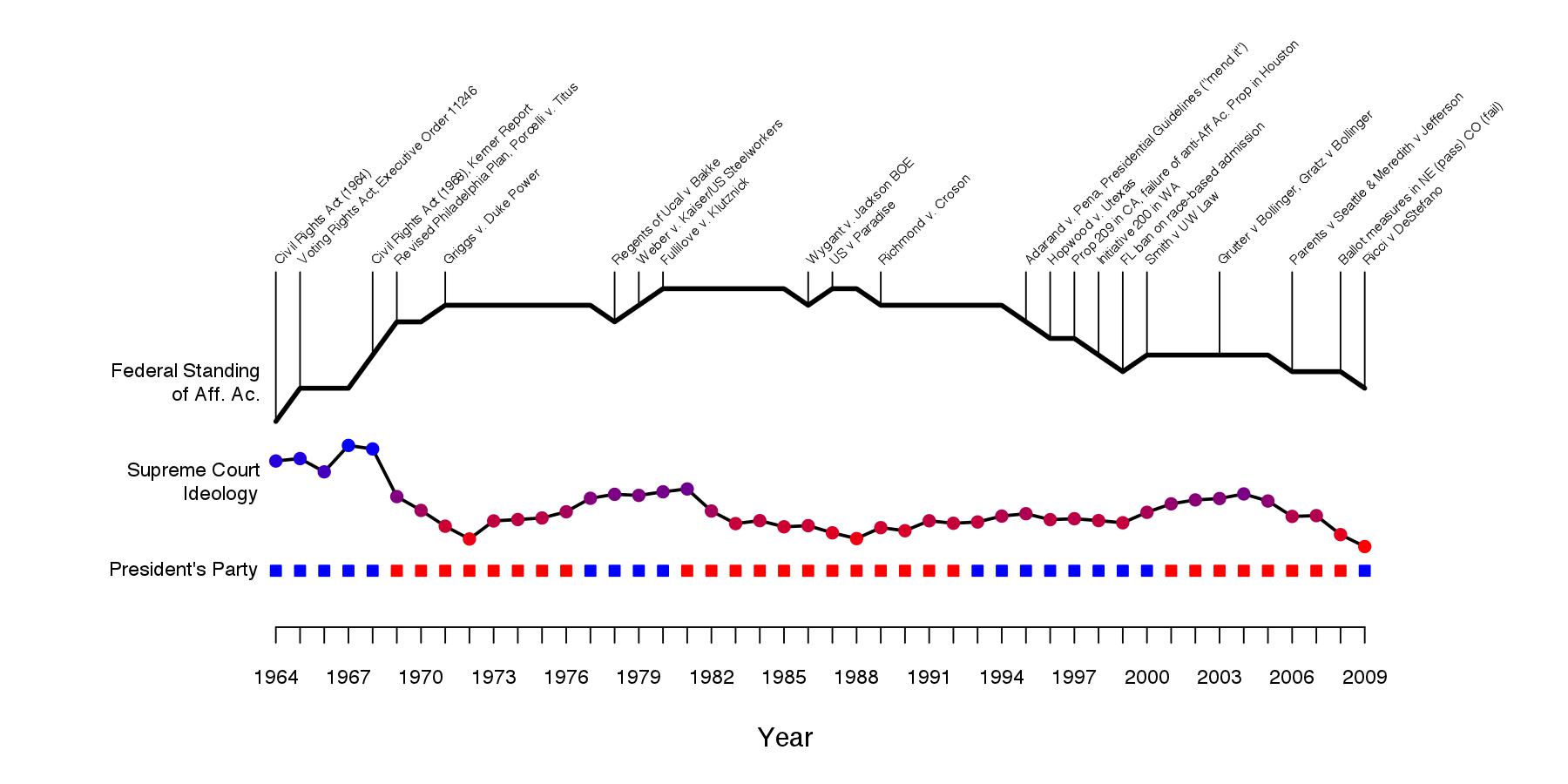
An heuristic visualization for use in my class on comparative political economy of affirmative action policies. Federal standing is scored simply by adding a point for each federal action or Supreme Court decision promoting the application of affirmative action, and subtracting a point for each action that curtails it. It is a gross simplification of course, but by appearances, it seems to capture the trends well. For example, while there have been steady curtailments since the early 1990s, it would be inaccurate to suggest federal standing is where it was at the time of enacting the Civil Rights Act in 1964. The federal level actions causing the score to increase or decrease are also shown.

Below the federal standing score is a plot of the Martin-Quinn score (link) of the median Supreme Court justice, a measure of the court’s liberal orientation (shown as blue, higher values) versus conservative orientation (red, lower values). Below that is a timeline of the party of the president.

John David Skrentny, in his magisterial account of the evolution of affirmative action politics in the US (link), highlights crisis management in the face of the race riots of the mid-1960s and US leadership’s concerns over international reputation during the Cold War as crucial determinants of affirmative action’s rise in that period. We can see that, at least by measure of party and court ideology, the institutional/ideological context was also especially receptive. At the same time, trends pushing upward the federal standing of affirmative action continued despite Nixon assuming office and a trend toward conservatism on the court.

“Tomorrow’s Africa is going to be an economic force,” says a report from Goldman Sachs. KPMG trumpets the Africa story as “the rise of the phoenix.” Many factors have made this possible. After decades of stagnation, in recent years most African countries began to reform their economies. Wars, coups, political instability and disease have declined since the late 1990s. And rising commodity prices have lured investment in African resources. Mobile technology is leapfrogging ahead (Africa has become one of the fastest-growing markets for Canadian firm Research in Motion’s BlackBerry) and a new consumer class has been born. Multinational retailers are leaping in, and even Wal-Mart recently acquired a chain with nearly 300 stores in 14 African countries. The prosperity of China has been a particular spark, with about 2,000 Chinese companies investing $32-billion in Africa by the end of 2010.

But what is the truth behind the hype?

On a continent with a long history of foreign domination and colonial exploitation, this wave of external investment has the potential to repeat some of the errors of the past. There is still a power imbalance between huge multinational investors and weak governments, with officials tempted by quick payoffs and sometimes willing to sell out the people who live on the land. Mining and oil companies can generate big sums of money for governments while employing less than 1 per cent of the African work force.

From the first installment of a six part series by Globe and Mail‘s Geoffrey York on Africa’s growth boom (link). It promises to be great.

“Growth elasticity of poverty” refers to percentage reduction in poverty per percent growth in average income (link). The concept can be extended to consider how access to infrastructure and services, access to legal protection, and other general features of development accompany a rise income. Analyses of growth such as that which Sierra Leone is experiencing (profiled in York’s article) ought to keep stock of such relationships.

Over the past year I’ve traveled quite rapidly through middle income and lower income countries in Asia, Latin America, and Africa, as well as middle and lower income areas in each of these countries. Naturally this has led to mental comparisons. One feature that sharply distinguishes the two contexts is the extent to which a local entrepreneur has some non-laughable chance of realizing and growing a market for an idea, even to the point of industrial level production. In reading York’s piece it is hard to see how the types of large scale extractive investments that Sierra Leone is hosting will promote local or national level entrepreneurship. So does development need to come from somewhere else, perhaps leveraging income from these investments, but not fundamentally drawing its momentum from it? If so, then in addition to tracking growth elasticity of development indicators, one would want to consider the proportion of income gains attributable to direct sale of extractive commodities versus through other transactions.

Drew Dimmery, a current NYU PhD student, has just finished coding up a new package for R that applies state-of-the-art non-parametric methods to estimate treatment effects for regression discontinuity designs. The package is now in beta, and we are looking for feedback from users. Drew has a nice description at his blog here: link. Drew also posted an introduction to the package to the POLMETH listserv: link.

Some great feedback has already come in, focusing in particular on possible problems with the Imbens-Kalynaraman bandwidth selection algorithm. If you have suggestions on improvements on that front, we are especially interested.

We are hoping to add more functionality to future versions (e.g., nonparametric covariate adjustment).

We would love to receive more feedback, whether in comments here, on Drew’s blog, or via email.

The International Initiative for Impact Evaluation (3ie) has an open call for proposals for researchers to replicate and extend the analysis of data from major development interventions and publications:

The primary objective of the replication programme is to improve the quality of evidence available for development policymaking and programme design. More specifically, the replication programme seeks to:

• Verify the findings, and examine the robustness of findings, in selected influential, innovative, or controversial impact evaluations of development interventions;
• Improve the incentives of researchers to conduct careful and responsible data analysis.

Completed replications will be published through the 3ie website and working paper series. In addition, a special issue of the Journal of Development Effectiveness will be published containing a selection of studies resulting from this first request for applications.

Details for this CFP are here: link. More details on 3ie’s replication program are here: link. Questions about the CFP need to be submitted by July 13, and applications need to be in by July 31. Note that this CFP is only about replicating data analyses, not replicating studies in their entirety. 3ie has prioritized a set of “candidate studies” for this round of replication funding: link.

I use this kind of data-analysis replication regularly in my teaching, and I applaud this effort. It would be particularly useful for researchers and graduate students considering either (i) designing new research that builds on the findings any of the candidate studies or (ii) new analytical methods that explore, e.g, effect heterogeneity, distributional effects, or violations of standard assumptions (e.g., violations of no interference assumptions). In either case, replication and exploration of the robustness of past findings would be a crucial first step. This is a chance to build that first step up and turn it into an output of its own.

[T]he true postcolonial age came to an end in the last quarter of the twentieth century. Since then, Africa has entered a phase in its history that as yet has no name. (We can’t call it ‘post-post-colonial’.)…Among the dynamic new factors shaping Africa’s environment in recent years are a rapid rise in foreign investment in Africa, particularly from Asia, although Western countries are still the leading investors in Africa, and large-scale immigration by Chinese entrepreneurs. It is already apparent that Asian businesspeople and diplomats do not come to Africa with the same expectations as their European and American counterparts, nor with the same ideological baggage, and that they make different demands…As African societies respond to new demands and as people develop new strategies, new forms of insertion in the world are emerging.

So writes Stephen Ellis in Season of Rain: Africa in the World (Hurst & Co., 2011), a panoramic account of how local interests across Africa interact with international business, development, and major power strategy. A dense read (counting 170 pages but feeling like 300), Ellis makes the case that African societies have had to contend with strong international currents despite state weakness. Thus, the most important types of exchange have been between international currents and familial and patronage networks operating in the “shadows” of the state. There are echoes of Reno and Bayart, but updated. The book is quite sweeping and sometimes fails to back assertions with clear references to data. But it would make an excellent read for undergraduates or others seeking an introduction to modern predicaments facing policy makers, business people, and ordinary folks across Africa as they contend with international actors pursuing their commercial, strategic, as well as development aid and humanitarian interests.