Regression discontinuity designs and missing data: some non-intuitive results

As with all sorts of data analysis scenarios, when you are carrying out a regression discontinuity (RD) study, you might have some missing data. For example, suppose you are using the (now, classic) Lee (2008) research design to estimate the effects of being elected to political office (ungated link; but note critiques of this design as discussed here: link). In this design, we exploit the fact that in plurality winner-take-all elections, there is an “as if” random aspect to the outcomes of elections that have very close margins of victory. E.g., a two-candidate race in which the winner got 50.001% of the vote and the loser got 49.999% is one in which one could imagine the outcome having gone the other way. Thus, using margin of victory as a forcing variable sets you up for a nice RD design. But, the rub is that you need data on both the winners and the losers in order to track the effects of winning versus losing. Unfortunately, it may be the case that data on the losers is hard to come by. They may drop out of the public eye, and so you will have a selected set of losers that you are able to observe. That is, you have missing outcome data on losers.

In a working paper in which I review semi-parametric methods for handling missing data, I discuss how inverse probability weighting (IPW), imputation, and their combination via “augmented” inverse probability weighting (AIPW) might be well suited to the task to dealing with missing data for RD designs (link to working paper). The problem with these methods, though, is that they rely on an “ignorability” assumption: that is, for the cases whose outcomes are missing, you nonetheless have enough other information on them to be able either (i) to predict well whether they are missing or (ii) to predict well what their outcomes would have been had they been observed. Ignorability is a strong and untestable assumption. Thus, in the paper I discuss very briefly the idea of doing sensitivity analysis to examine violations of ignorability.

I am currently re-working that paper, and in doing so working out how exactly such a sensitivity analysis ought to be carried out. As a useful prompt, I received an email recently asking precisely what one might do to study sensitivity to missing data in the RD scenario. My proposal was that one could do a couple of things. First, one could compute bounds based on imputing extreme values for the missing outcomes, and seeing what that suggests. This would be along the lines of a Manski-type “partial identification” approach to studying sensitivity to missing data (see Ch. 2 in this book: link). Second, one could do an IPW adjusted analysis (keeping to the side imputation and AIPW for the moment), and see how your results change. Third, one could do a sensitivity analysis for the IPW analysis. A sensitivity analysis that I imagine is to take the complete cases and residualize their outcome variable values relative to the forcing variable and any other covariates used to predict the missingness weights. Then, scale these residuals relative to the strongest predictor of missingness (determined, for example, using a standardized regression analysis). And finally, examine the consequences of increasing the influence of these scaled residuals in predicting missingness. Then, you would have a way to examine sensitivity to ignorability in a manner that is scaled to the strongest predictor and its influence.

These suggestions were a bit off the cuff, although they made intuitive sense. Nonetheless, I wanted to check myself. So I did a toy simulation. The findings were surprising.

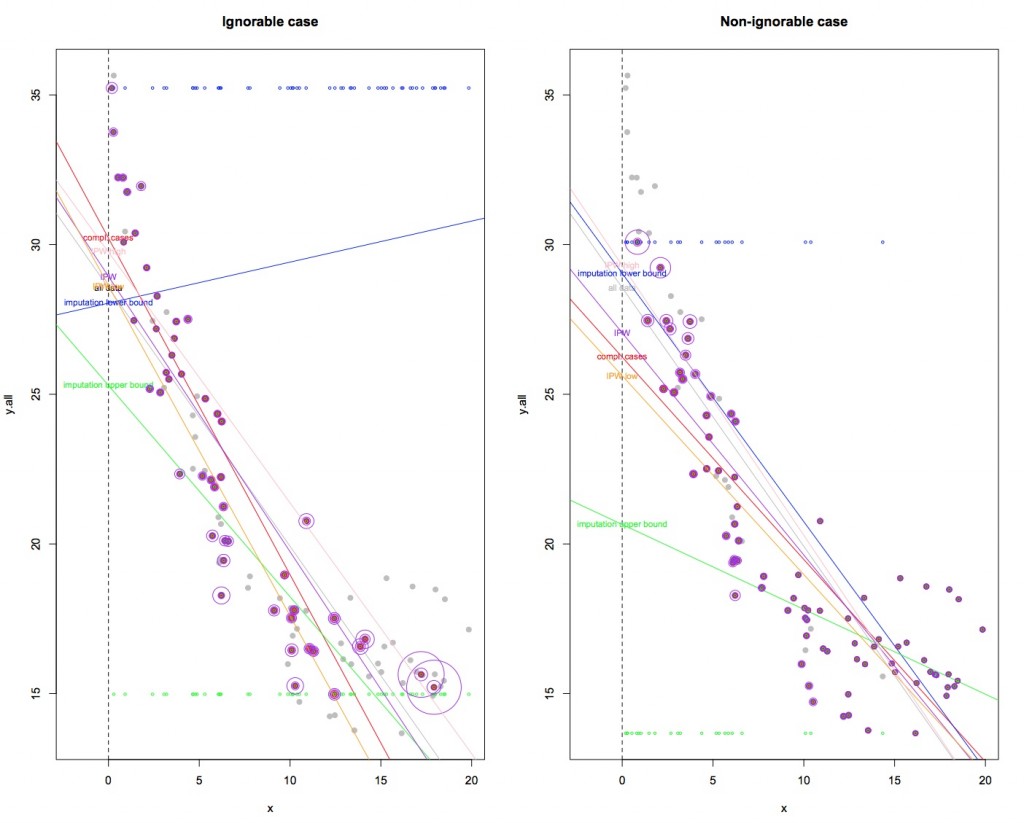
The R code for the toy simulation is here: R code.[1] The code contains two examples of trying to predict an intercept value using a local linear approximation to a non-linear relationship. This is one side of what one is trying to do in a standard RD analysis. In one example, ignorability holds, and in the other it does not. Ideally, what I would like you to do is to run that code line by line in R and look at the graphical output that shows the result of each approach to addressing the missing data problem. The steps include, first computing a benchmark prediction that would obtain were there no missingness (“all data” scenario). Then, we look at predictions resulting from,

(1) doing nothing — aka, complete case analysis (“compl. cases” scenario);
(2) imputing extrema (“imputation lower bound” and “imputation upper bound”, where lower and upper are referring to whether min or max values are imputed);
(3) IPW adjustment (“IPW”), and then
(4) an IPW sensitivity analysis along the lines discussed above (“IPW low” and “IPW high”).

For those who can’t run the code, here is a (very crowded) PDF that graphs color-coded results for the two examples: PDF. You will have to zoom in to make sense of it. It shows where all the predictions landed. We want to be in the neighborhood of the intercept prediction labeled “all data”.

Here are the basic conclusions from this toy simulation. First, and most importantly, the bounds from imputing extrema don’t necessarily cover what you would get if you had all the data! This occurred in the ignorable case. This was surprising to me and it’s worth considering more deeply. The problem is due to the fact that one is trying to predict an intercept here, and so imputing high or low values for the missing data does not necessarily imply that the resulting intercept estimate will cover what you would get with the full data. It seems that the linear approximation to the non-linear relationship is compounding the problem, but that is a conjecture that needs to be assessed analytically. I found this quite interesting, and it suggests that what we know about sensitivity analysis for simple difference in means types estimation does not necessarily travel to the RD world.

Second, the IPW sensitivity analysis is pretty straightforward, and works as expected. However, it requires that you choose—more or less, out of thin air—what defines an “extreme” violation of ignorability. Also, the IPW sensitivity analysis still leaves you with a fairly tight range of possible outcomes. This is not necessarily a good thing, because the tightness might imply that there are still some assumptions that aren’t being subjected to enough scrutiny. So I think this is a promising approach, but probably needs a lot of consideration and justification when used in practice.

Third, in these examples, IPW always removed at least some of the bias, although there are cases where this may not happen (see p. 21 of my paper linked above for an example).

So there are some interesting wrinkles here, the most important being that Manski type approaches may not travel well to the RD scenario. I need to check to be sure I’m not doing something wrong, but assuming I didn’t that’s an important take-away.

[1] Okay, the code is pretty rough in that lots of things are repeated that should be routinized into functions, but you know what? I never claimed to be a computer programmer. Just someone who knows enough to get what I need!