I wanted to look into the case where you have an experiment in which your units of analysis are naturally clustered (e.g., households in villages), but you randomize within clusters. The goal is to estimate a treatment effect in terms of difference in means, using design-based principles and frequentist methods for inference.
Randomization ensures that the difference in means is unbiased for the sample average treatment effect. Using only randomization as the basis for inference, I know the variance of this estimator is not identified for the sample, as it requires knowledge of the covariance of potential outcomes. But the usual sample estimators for the variance are conservative. If, however, the experiment is run on a random sample from an infinitely large population, then the standard methods are unbiased for the mean and for the variance of the difference in means estimator applied to this population (refer to Neyman, 1990; Rubin, 1990; Imai, 2008; for finite populations, things are more complicated, and the infinite population assumption is often a reasonable approximation). I understand that these are the principles that justify the usual frequentist estimation techniques for inference on population level treatment effects in randomized experiments.
The question I had was, how should we account for dependencies in potential outcomes within clusters? The cluster-randomized-experiments literature has made it clear that when the treatment is applied at the cluster level, we certainly need to account for the clustering. This is made explicit by the Moulton factor, which measures the ratio of the true standard deviation of the difference in means with clustered data to a standard error estimate that ignores the clustering. The Moulton factor is given by the square root of the following expression (from Angrist and Pischke, 2008:311),
[latex]
\frac{V(\hat{\beta})}{V_c(\hat{\beta})} = 1 + \left[\frac{V(n_g)}{\bar{n}}+\bar{n} -1\right]\rho_x\rho_e,
[/latex]
where $latex V(\hat{\beta})$ is the true variance of the differences in means estimator, $latex \hat{\beta}$, $latex V_c(\hat{\beta})$ is the limit of the variance estimator that ignores the clustering, $latex n_g$ refers to cluster size and $latex \bar{n}$ is the average cluster size, and $latex \rho_x$ and $latex \rho_e$ are the (Kish-type) intra-class correlations for the treatment variable and deviations from predicted means (i.e., the residuals if the difference in means is computed with OLS).
From this expression, it would seem that the randomization within clusters would render the need for cluster adjustment unnecessary, given that randomization within clusters ensures that the intra-class correlation of the treatment variable ($latex x$) is zero.
But this runs contrary to another intuition: The standard error for your mean estimate for the treated probably needs to take into account the dependence among treated groups within each cluster, and the same is true for your mean estimate for the controls. Heuristically, a more useful summary might be the intra-class correlation among treated units, grouped by cluster, and control units grouped by cluster. Treatment status is constant within those subgroups in each cluster, and so the $latex \rho_x$ equals 1. In that case, substantial residual dependence, measured by the $latex \rho_e$ term, should have some bite.
In lieu of working this out analytically, I came up with some simulations to study the performance of cluster robust standard errors (CSEs) versus heteroskedasticity robust standard errors (HSEs) in this situation. In principle, if there is meaningful within-cluster dependence, the CSEs should be bigger than the HSEs, although the opposite may occur in any given sample. So I also looked into the performance of $latex \max(\text{CSE, HSE})$, which I will call “conservative” CSEs (CCSEs). To generate the dependence structure, I constructed potential outcomes as draws from a multivariate normal distribution:
$latex \left[ \begin{array}{c} Y^1_{1g}\\ \vdots \\ Y^1_{Mg} \\ Y^0_{1g}\\ \vdots \\ Y^0_{Mg} \end{array} \right] \sim \text{MVN}(\mathbf{0}, \left[ \begin{array}{cc} \Sigma_{11} & \Sigma_{10}\\ \Sigma_{10} & \Sigma_{00} \end{array} \right] )$,
where $latex g$ indexes clusters of size $latex M$, $latex Y^1_{gm}$ is the potential outcome under treatment for unit $latex m$ in group $latex g$ and $latex Y^0_{gm}$ is the potential outcome for that unit under control, $latex \Sigma_{11}, \Sigma_{10}, \Sigma_{00}$ specify potential outcomes covariances among treated units, across treated and control units, and among control units, respectively. I kept these matrices simple, with variances for all potential outcomes fixed to 1. I looked into different values for the correlation across potential outcomes for a given unit. I fixed this to $latex \rho_{10,i}$ for all units (the diagonal of $latex \Sigma_{10}$ is an array with this term). I also looked at different values for within-cluster dependence, using common values for the off-diagonals in all three matrices. Call the correlations in the off diagonals, $latex \rho_{1,ij}, \rho_{10, ij}$, and $latex \rho_{0,ij}$, standing for within-cluster correlation between (i) different treated units, (ii) across treated and control outcomes for different units, and (iii) between different control units, respectively. All clusters were given the same covariance structure. A “placebo” treatment was assigned to units via a design that randomly assigned 1/2 of units to treatment within each cluster (i.e., it was a unit-level randomized design blocked by cluster; it was not a cluster-randomized design). The placebo treatment has no causal effect, and so the “true” average treatment effect in this simulated experiment is 0.
For the simulations, I fixed the group size ($latex M$) to 10 and the number of groups ($latex G$) to 50 for a total sample of 500. I estimated the average mean difference using OLS. Standard errors were computed as Stata-style finite-sample-adjusted robust standard errors. Specifically, let $latex X$ stand for a matrix that contains the treatment assignment vector in the first column and a vector of ones in the second, and let $latex x_{gm}$ and $latex e_{gm}$ stand for the covariate values and OLS residual for unit $latex m$ in group $latex g$, respectively. Then, HSEs were computed as the square roots of the diagonals of,
$latex \frac{GM}{GM-2}(X’X)^{-1} \left( \sum_{g=1}^G \sum_{m=1}^M x_{gm}x_{gm}’ e_{gm}^2 \right)(X’X)^{-1}$
and CSEs were computed as the square roots of the diagonals of,
$latex \frac{G}{G-1}\frac{GM-1}{GM-2}(X’X)^{-1} \left( \sum_{g=1}^G X_g’ e_g e_g’X_g \right)(X’X)^{-1}$
CCSEs were computed as the maximum of the two. I evaluated the standard error corresponding to the treatment variable.
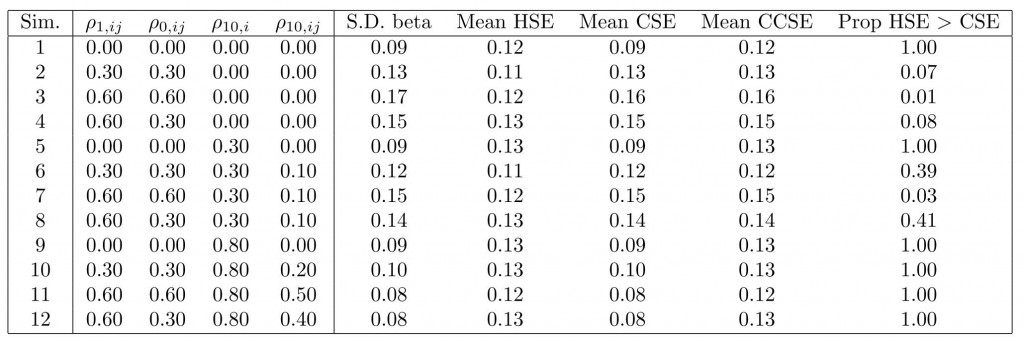
The table below shows the results from 5,000 runs on different covariance parameter settings. (In all cases, the OLS estimator was unbiased, as expected, so I don’t report that.) The column labeled “S.D. beta” gives the empirical standard deviation of the difference in means estimates. That is our benchmark “truth” against which we compare the different standard error estimates.
Whenever there is any cluster dependence, the HSEs perform poorly. For the most part, the CSEs are reliable, although they are not appreciably more reliable than the CCSEs. Indeed, only when we have quite high levels of correlation between unit potential outcomes do they tend to be over-conservative, and even in these cases, the degree of conservatism is not so high on average. Furthermore, in simulations 1, 5, and 9, where HSEs and CSEs should be equal asymptotically, we see that in the majority of cases, CSEs are smaller than HSEs. In such cases, CSEs are anti-conservative (with respect to Type I error). By construction, the CCSEs do not suffer this problem. Thus, if one’s primary concern is to avoid Type I error, CCSEs are a good choice.
Thus, in answering our question above, it is clear that yes, we do need to account for the clustering, and to deal with finite sample issues, CCSEs are an appealing option. This is actually in line with what Angrist and Pischke recommend when discussing clustered data.
As a second conclusion, it seems the intuition derived from inspecting the Moulton factor here is incorrect. Why might this be the case? Is it because the original derivation is based on a random unit effects model for which, indeed, if we have balance over treatment assignment, then these unit effects will cancel? If so, under more general types of cluster dependence, this cancellation will not occur. Any thoughts on that would be appreciated!
UPDATE:
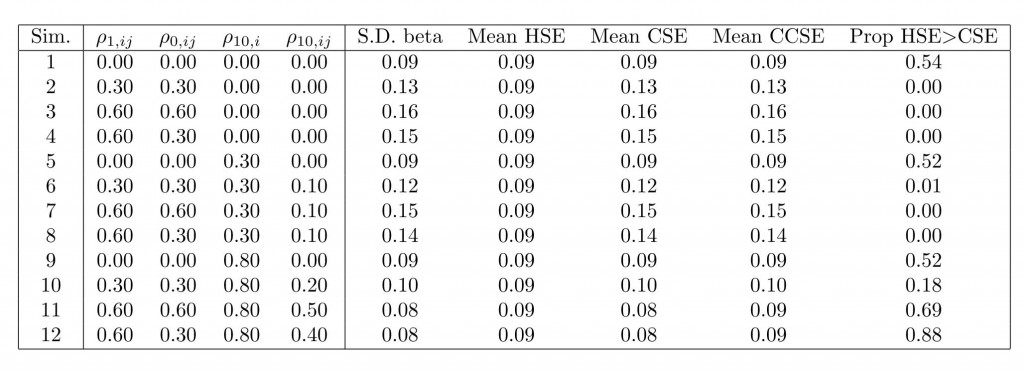
Responding to WL’s excellent comments below, I tried another set of simulations. They are similar to what WL suggested in “scenarios two and three,” although rather than using additive village “shocks” I induce dependence via the covariance matrix directly, as discussed above. The difference with the previous simulations is that, rather than having potential outcomes for all groups have a mean of 0, I allowed the group means to vary. To do so, I drew $latex G$ group means, $latex \alpha_1,\hdots,\alpha_G$, independently from $latex \text{N}(0,1)$ and then fixed these group means over all simulation runs. Thus, all potential outcomes for group $latex g$ have mean $latex \alpha_g$ over all simulation runs. This in itself induces an intra-cluster correlation of about 0.5 (recall variances were 1 for all potential outcomes). Then, potential outcomes were drawn using the within-cluster dependence structure described above. Here are the results:
In this simulation, using the CCSEs comes at a heavier price than before. When there is either no substantial dependence beyond the group fixed effects (simulations 1, 5, and 9), or if there is substantial dependence between unit-level potential outcomes (simulations 10, 11, and 12), CCSEs strike me as too conservative now. The CSEs continue to perform quite well on average. Simulations 1, 5, and 9 are similar to WL’s scenario two, but note here that the CSEs are much preferable to the HSEs, which wasn’t expected.
(Of course, this assumes no coding errors! If you want to check it out for yourself, here is the simulation code (for R): link .)

Cyrus, either of these inference scenarios could be defensible:
1) The villages are a simple random sample from a much larger population, and you want inference about the larger population.
2) You’re content with inference about the specific villages where you have data. Also, you aren’t claiming to generalize to what might have happened if the villages had experienced different economic shocks, etc.
Your simulations seem appropriate for #1, whereas the Moulton-factor intuition seems right for #2.
For #2, you could do a simulation where E(Y1) and E(Y0) vary across villages but are fixed across runs, and within each village, Y1 and Y0 are i.i.d. across households.
If you’re interested in a third scenario, with fixed villages but random economic shocks, you could simulate each village’s E(Y1) and E(Y0) as the sum of (i) a component that varies across villages but is fixed across runs and (ii) a random village-level shock. Then in general, neither the HSE nor the CSE will give the right answer; the data from one run won’t identify the variance of the shock.
Just a side note: When the probability of treatment is 1/2, the traditional non-robust OLS standard error should perform at least as well as the HSE.
WL: great comments. You are right, these simulations are mostly like your scenario 1. See the update to the post above for examination of your scenarios 2 and 3.