At the APSA meeting this past week I discussed a very nice working paper by Blackwell, Ma, and Opacic on testing potential causal mechanisms. Their paper enumerates the assumptions needed to justify the “intermediate outcome test”—that is, the common practice of estimating treatment effects on a mediator variable (an intermediate outcome) to test whether a proposed causal mechanism is plausible: [arxiv].
Considering the case of a binary mediator, without an assumption that the treatment effect on the intermediate outcome is monotonic, this test is not necessarily informative. You could estimate a zero average treatment effect on the mediator but the mechanism could still be active. A zero average treatment effect on the mediator could mean either that the treatment does not affect the mediator for anyone, or that the treatment has a positive effect for some and a negative effect for others, and these effects cancel out. The issue is apparent in the following expression from Blackwell et al.’s paper for the average natural indirect effect (ANIE, also known as the average causal mediation effect):
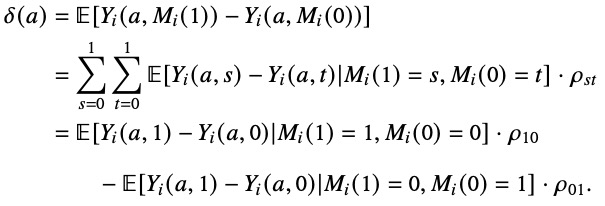
where delta(a) is the ANIE and M(a) is the potential mediator value when treatment A=a, Y(a,s) is the potential outcome when treatment A=a and mediator M=s, and then we have rho_10 and rho_01 as the probabilities that the effect of the treatment (A) on the mediator (M) is positive or negative, respectively. This expression is non parametric and a simple consequence of applying total probability. The average treatment effect on the mediator is equal to rho_10 – rho_01. You could have rho_10 = rho_01 \ne 0, in which case you would have zero average treatment effect on the mediator, but still have a potentially non-zero ANIE.
Now, the intermediate outcome test is motivated by the intuition that the mediation effect can sometimes be written as the product of the effect of the treatment on the mediator and the effect of the mediator on the outcome. From the expression above, you can see that the ANIE can be written as such a product when the conditional effects are equal, i.e., E[Y(a,1) – Y(a,0) | M(1) = 1, M(0) = 0] = E[Y(a,1) – Y(a,0) | M(1) = 0, M(0) = 1] = B, in which case the expression reduces to B*(rho_10 – rho_01). This assumption of effect homogeneity (across groups for which the effect on the mediator is positive or negative) seems pretty strong though, right?
Indeed, it is strong, and, at least a conditional-on-covariates version of it is an implication of sequential ignorability as stated in, e.g., Imai et al. (2010):
Personally, I had not given much thought to how the second part of the assumption (expression 5), by imposing restrictions across outcome and mediator potential outcomes, implied effect homogeneity across types defined in terms of how the treatment affects mediator values. If we consider the analogy to instrumental variables, this would be like restricting causal effects to be homogenous across compliers and defiers.
Once one appreciates this implication of sequential ignorability, other things can follow, such as using estimates of conditional effects to identify mediation effects, as in this paper by Fu: [arxiv].
I guess the question is whether we are willing to accept such restrictions on effect heterogeneity in the first place, and if not, whether we are willing to accept other restrictions on effects, such as monotonic effects of the treatment on the mediator. The answer depends on the application, but in any case these papers are important for clarifying what kinds of assumptions you need to defend.
