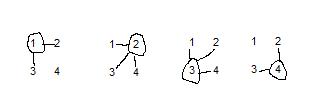Cyrus Samii

Forthcoming in Statistics and Probability Letters are results by Peter Aronow and myself on how heteroskedasticity-robust and homoskedasticity variance estimators for regression coefficients relate to the exact randomization variance of the difference-in-means estimator in a randomized experiment.

The gated link is here (link). For those without access to the journal, contact me for a copy.

The main results are that the ol’ White heteroskedasticity-robust variance estimator (aka, “, robust”) yields a conservative (in expectation) approximation to the exact randomization variance of the difference-in-means for a given sample, and estimates precisely the randomization variance of the difference-in-means when we assume that the experimental sample is a random sample from some larger population (the “super-population” interpretation). There are two slight tweaks though: (1) the exact equivalency is for the “leverage corrected” version of White’s estimator, but the difference between this version and White’s original version is negligible in all but very small samples; (2) because of Jensen’s inequality, these nice results for the variance don’t necessarily translate to their square root — a.k.a., your standard errors — but the consequences shouldn’t too horrible. The take-away, then, is that experimenters can feel okay about using “, robust” to obtain standard errors for their average treatment effect estimates in randomized experiments (assuming no cluster randomization, which would require other kinds of adjustment).

We also show that in the special case of a randomized experiment with a balanced design (equal numbers of treated and control), all sorts of estimators — including the heteroskedasticity-robust estimator, homoskedasticity estimator, and “constant effects” permutation estimator — are actually algebraically equivalent! So balance between treatment and control group sizes is a nice feature because of the way that it eases variance estimation.

The always illuminating Development Impact Blog (link) posts a synopsis of a nice paper by Jing Cai on social network effects in the take up of weather insurance in China (link). Social network effects are identified via a nice experimental design, which I’ll paraphrase as follows: financial education and insurance offers are given to a random subset of individuals in year 1. Then in year 2, insurance offers are given to the rest of the individuals. Social network effects on year 2 targets are measured in terms of their take-up rate as a function of the fraction of their friends that had been targeted in year 1. Positive social network effects correspond to a positive relation between year 2 take-up and the fraction of one’s friends having been targeted in year 1. The icing on the cake is that experiment also randomized the price of insurance offers, and could therefore translate the social network effect into a price equivalent, findings that the “effect is equivalent to decreasing the average insurance premium by 12%.”

One concern that I am not sure is addressed in the paper is a potential selection bias that can arise due to differences in individuals’ network size. To see how this works, consider a toy example. A community consists of 4 people labeled 1, 2, 3, and 4. Graphs of the friendship networks between these people are as follows: Person 1 is friends with 2 and 3, person 2 is friends with 1, 3, and 4, and so forth.

Suppose that in year 1, 2 out of these 4 are randomly assigned to receive an intervention. That yields 6 possible year 1 treatment groups, each equally likely: {1,2}, {1,3}, {1,4}, {2,3}, {2,4}, or {3,4}. As in the paper discussed above, suppose what we are interested in is the effect of some fraction of your friends receiving the year 1 treatment. We can compute what these fractions would be under each of the year 1 treatment assignments. With these, we can compute the propensity that a given fraction of a person’s friends received the year 1 treatment. These calculations are shown in the following table:

What this shows is that simple randomization of year 1 assignment does not result in simple random assignment of fractions for the year 2 analysis. Take person 1, for example. This person has a 2/3 chance of having half of her friends targeted in year 1, and a 1/3 chance of having all of her friends targeted. This is in contrast to person 2, who has no chance of having either half or all friends targeted. The design does not result in representative samples of people receiving the different fraction values. Examining differences conditional on fraction values does not necessarily recover causal effects because the populations being compared are not exchangeable. To justify a causal interpretation, one would have to assume that network structure is ignorable or that such ignorability could be achieved through covariates, etc. The problem arises because fraction value is a function of both a person’s friendship network and the year 1 assignment. Only one of those two elements is randomized.

Peter Aronow and I have generalized this issue in a paper on “Estimating Causal Effects Under General Interference.” A recent working draft that we presented at the NYU Development Economics seminar is here: link. The basic idea behind the methods that we propose are to (1) define a way to measure direct and indirect exposures, (2) determine how for each unit of analysis the design induces probabilities of different kinds of exposures, and (3) use principles from unequal probability sampling to estimate average causal effects of the various direct and indirect exposures. Another point that arises from the analysis is that you can use the propensities of different exposures to assess the causal leverage of different designs. For example, consider again the toy example above. Suppose that these four units constitute one cluster among many possible clusters. Conceivably, a design that randomized not only which people were targeted in the first round within a cluster but also how many were targeted from cluster to cluster could produce fraction value propensities that were equal or, short of that, at least ensured that everyone had some probability having each of a variety of fraction values.

Monitoring and Evaluation in Post-Conflict and Fragile States
Methods, experiences from the field, industry initiatives, challenges 

SPEAKERS

KELLY BIDWELL, Director of Post-Conflict Recovery Initiative, Innovations for Poverty Action

CYRUS SAMII, Assistant Professor, New York University

Tuesday, November 15, 6:00 pm
Room IAB 413, Columbia University – SIPA
Refreshments will be provided

Presented by SIPA’S MONITORING & EVALUATION STUDENT SOCIETY (MESS)
Co-organized with the Earth Institute’s AC4 ADVANCED CONSORTIUM ON COOPERATION, CONFLICT AND COMPLEXITY

Recently received:

The National Institute of Statistical Sciences (NISS) and the American Institutes for Research (AIR) announce the creation of a joint postdoctoral fellowship program focused on problems and issues arising from the design and analysis of complex surveys. The initial term of appointment will for two years, beginning early in 2012.

The Postdoctoral Fellow’s primary activity will be to carry out research on statistical theory, methodology and applications, addressing such areas as sample design, statistical methods, analysis of complex sample data, longitudinal surveys, model-based methods, multi-mode surveys, imputation, nonresponse, and data confidentiality. Contexts for the research include Project TALENT (see www.projecttalent.org), multiple activities in education stemming from AIR-NISS partnerships in efforts supporting the National Center for Education Statistics, and health—a strength of AIR and a significant interest of NISS. The Fellow will collaborate with and be mentored by NISS Director Alan Karr, NISS Assistant Director Lawrence Cox and statistical and domain scientists from AIR. Like the 75+ past and present NISS postdocs, the NISS-AIR Postdoctoral Fellow will play an innovative, leading role in the research, focusing it and even re-orienting it when necessary. She or he Fellow will engage in both ongoing projects and preparation of proposals for new ones.

The NISS-AIR Postdoctoral Fellow will be appointed by NISS, and will be located at AIR facilities in Washington, DC. He or she will be part of both the nationwide AIR community and the Washington- and Research Triangle Park, NC-centered NISS community. For more information about NISS and AIR, please see their web sites (www.niss.org and www.air.org).

Applicants must have received, or expect to complete, a doctorate in 2006 or later. Women and members of under-represented groups are particularly encouraged to apply. Criteria for selection include demonstrated research ability in statistics or an allied scientific discipline, interest in high-impact survey research, strength in computation, commitment to collaborative research, and excellent skills in verbal and written communication. The initial salary is $80,000 per year.

Applications should consist of (1) a letter of interest responding to the research emphases and criteria above and containing full contact information and citizenship/immigration status; (2) a CV that lists educational background, research experience and publications; and (3) abstracts of the dissertation and any publications. These items must be submitted electronically (as PDF files if possible) to [email protected]. Applicants should also arrange for three letters of reference to be sent to the same E-mail address, to which queries about the position, about NISS or about AIR may also be directed.

The deadline for full consideration is December 31, 2011. Later applications will be considered as resources permit. The appointment may be made at any time.

Job posting from our friends at the Columbia University Center for the Study of Development Strategies (link):

International Rescue Committee: Job Opening in Congo as CDR Evaluation Quality Manager

The CSDS team is undertaking a large evaluation in the Congo. Our partner – the International Rescue Committee – currently has a job opening for an Evaluation Quality Manager. The person would support the evaluation that tries to understand the impact of one of Africa’s largest community development projects. He or she will be responsible for liaising between the IRC team implementing the program and the team at Columbia leading the research design. He or she would support quality integration of research variables into program delivery. This includes piloting tools and instruments integrated into the program, training field staff, assisting and monitoring data collection at the grassroots level throughout Eastern DRC, conducting basic data analysis and writing up results.

More information here: PDF: IRC Position in Congo – CDR Evaluation Quality Manager.

The position is probably especially well suited for somebody planning to do a PhD – it is a perfect way to get field experience and learn the ins and outs of evaluation work.