The always illuminating Development Impact Blog (link) posts a synopsis of a nice paper by Jing Cai on social network effects in the take up of weather insurance in China (link). Social network effects are identified via a nice experimental design, which I’ll paraphrase as follows: financial education and insurance offers are given to a random subset of individuals in year 1. Then in year 2, insurance offers are given to the rest of the individuals. Social network effects on year 2 targets are measured in terms of their take-up rate as a function of the fraction of their friends that had been targeted in year 1. Positive social network effects correspond to a positive relation between year 2 take-up and the fraction of one’s friends having been targeted in year 1. The icing on the cake is that experiment also randomized the price of insurance offers, and could therefore translate the social network effect into a price equivalent, findings that the “effect is equivalent to decreasing the average insurance premium by 12%.”
One concern that I am not sure is addressed in the paper is a potential selection bias that can arise due to differences in individuals’ network size. To see how this works, consider a toy example. A community consists of 4 people labeled 1, 2, 3, and 4. Graphs of the friendship networks between these people are as follows:
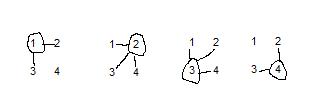Person 1 is friends with 2 and 3, person 2 is friends with 1, 3, and 4, and so forth.
Suppose that in year 1, 2 out of these 4 are randomly assigned to receive an intervention. That yields 6 possible year 1 treatment groups, each equally likely: {1,2}, {1,3}, {1,4}, {2,3}, {2,4}, or {3,4}. As in the paper discussed above, suppose what we are interested in is the effect of some fraction of your friends receiving the year 1 treatment. We can compute what these fractions would be under each of the year 1 treatment assignments. With these, we can compute the propensity that a given fraction of a person’s friends received the year 1 treatment. These calculations are shown in the following table:
What this shows is that simple randomization of year 1 assignment does not result in simple random assignment of fractions for the year 2 analysis. Take person 1, for example. This person has a 2/3 chance of having half of her friends targeted in year 1, and a 1/3 chance of having all of her friends targeted. This is in contrast to person 2, who has no chance of having either half or all friends targeted. The design does not result in representative samples of people receiving the different fraction values. Examining differences conditional on fraction values does not necessarily recover causal effects because the populations being compared are not exchangeable. To justify a causal interpretation, one would have to assume that network structure is ignorable or that such ignorability could be achieved through covariates, etc. The problem arises because fraction value is a function of both a person’s friendship network and the year 1 assignment. Only one of those two elements is randomized.
Peter Aronow and I have generalized this issue in a paper on “Estimating Causal Effects Under General Interference.” A recent working draft that we presented at the NYU Development Economics seminar is here: link. The basic idea behind the methods that we propose are to (1) define a way to measure direct and indirect exposures, (2) determine how for each unit of analysis the design induces probabilities of different kinds of exposures, and (3) use principles from unequal probability sampling to estimate average causal effects of the various direct and indirect exposures. Another point that arises from the analysis is that you can use the propensities of different exposures to assess the causal leverage of different designs. For example, consider again the toy example above. Suppose that these four units constitute one cluster among many possible clusters. Conceivably, a design that randomized not only which people were targeted in the first round within a cluster but also how many were targeted from cluster to cluster could produce fraction value propensities that were equal or, short of that, at least ensured that everyone had some probability having each of a variety of fraction values.
My intuition was: so long as the treatment has no direct effect on network structure, you should be in the clear no? Seems like a standard IV argument holds, right?
Thanks for the reply, Pete. I don’t think it’s that innocuous though. Consider the toy example above. Suppose that this group of 4 units is copied a bunch of times, and within each copy the same experiment is run. When we get our data, we’ll have people with fraction values of 1/2, 2/3, and 1. But the 1/2 and 1 fraction values will always be assigned to people with 2 friends, and the 2/3 fraction values will always be assigned to people with 3 friends. So, at least on the covariate of number of friends, you don’t have balance. To the extent that number of friends is associated with the outcome, you have a confound. Conditioning (e.g., via regression) would imply extrapolating (e.g., extrapolating to cover the lack of data for outcomes at 1/2 or 1 for people with 3 friends). You can’t match because there’s no overlap. Now, these issues are pretty extreme in the toy example. But they generalize, perhaps in a less extreme manner but nonetheless, to a more general set-up with larger clusters, more friends, etc.
Thanks. If I understand correctly then, the concern is that individuals’ networks are not randomly assigned, so that someone with a 2/3-fraction treated may differ from someone with 1/3 treated. You mention conditioning, which seems to make sense–akin to conditioning on ‘risk sets’ when there’s multiple lotteries–but then I suppose there’s the issue of whether you expect effects to be heterogeneous by network structure. It seems like in a large sample however, you could tease this out? Curious to know what you think. I’ll certainly read through your paper as well.
Thanks for highlighting this issue. (I like you paper with Peter.)
This same problem comes up in my work. However, if one has larger degree and conditions on degree, my understanding is that this problem goes away.
Also, I wonder whether fraction of peers assigned is really the best way of parametrizing the treatment. Absolute number of peers is an alternative. If one conditions on each unique degree value, this question looses some of its import, but this often isn’t so possible.
At least some of the trouble in your example comes from the negative dependence in your assignment mechanism (ie you aren’t using simple random assignment).
Thanks, Dean. I agree on your points. The small network in the toy example amplifies the problem. In examples where the networks of interest are defined as groups of friends in small communities, it might not be such a bad approximation though. I also wonder whether fraction is the best way to go about it. Finally, on the negative dependence, indeed if the assignment were more like a Bernoulli process, where each person had an independent chance of being assigned to treatment, then we would get better overlap in the propensity scores, meaning that non-parametric identification would be possible in this example, but not without accounting for the differences that would nonetheless arise in the values of the propensity scores.
Pete – apologies for not having replied earlier to your query. Yes, you could tease that out so long as the design produced enough random variation in fraction values conditional on network structure values (e.g., number of friends). The design that I proposed where number of year 1 treated varies randomly from locality to locality would accomplish that. The Bernoulli assignment (essentially treatment assigned for each unit independently with a weighted coin flip) idea in the previous comment would accomplish it in expectation, although it might be better to fix this variation by design because the Bernouilli assignment would produce unpredictable assignment profiles in moderately sized studies.