At a talk recently on new methods for inverse probability weighting for missing data, I put up the following picture, provoking the consternation of a few people in the room:
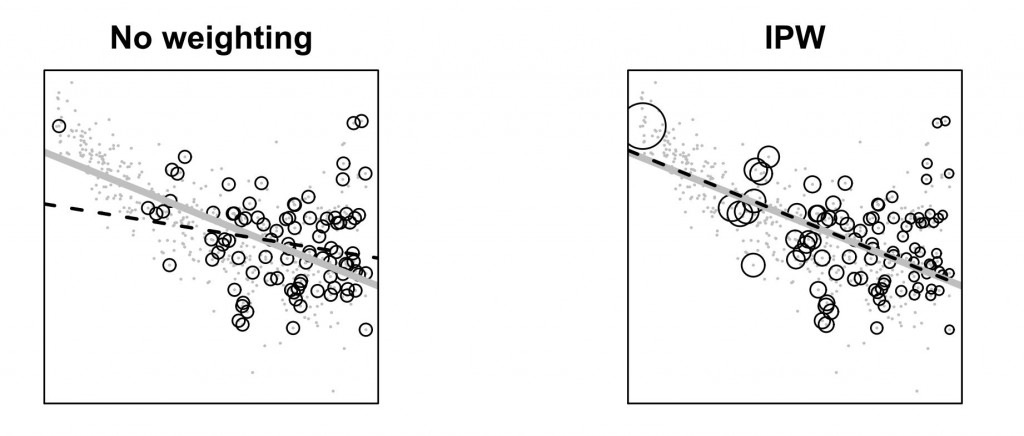The little gray dots on both graphs are the same scatter plot from a population for which the relationship between the x-axis variable and the y-axis variable exhibit a non-linear relationship. The gray line on both graphs is a linear OLS fit to this nonlinear relationship, which by definition is the best linear approximation in terms minimizing squared deviations. The hollow circles show data that are sampled with unequal probabilities from this underlying population of gray dots. The departure from simple random sampling is that the probability of inclusion is increasing simply in the values of the x-axis variable. The black dashed line on the graph to the left is the linear OLS fit to the non-random sample. The black dashed line on the graph to the right is a weighted linear OLS fit, where the weights are equal to the inverse of the predicted probabilities of inclusion in the sample taken from a logistic regression of an inclusion indicator on the x-axis variable. The size of the weights for each observation is proportional to the size of the hollow circles in the right graph.
The picture is meant to illustrate a few things: (1) that the x-axis variable contains two features, one that relates to the y-axis variable, and another separate feature that relates to an indicator for inclusion in the sample, and that these features are not redundant; (2) that using the information from the second feature of the x-axis variable allows us to recover the population-level linear approximation; and (3) that we should not trust the usual textbook advice that we get about departures from random sampling (or, when the goal is causal inference, random assignment), which says that so long as our model includes the variables that explain the departures from equal probability sampling, we can ignore such departures. Clearly the usual textbook advice assumes that the model is correct, which is something that can be verified in only the simplest cases. The picture above might be such a simple case, but for higher dimensional problems, such may not be the case. Thus, what the picture shows is that inverse probability weighting allows us to recover an approximation, so long as the inverse probability weights are accurate. This is half of the “double robustness” property of inverse probability weighted estimators. Insofar as it is relatively easier to model the sample inclusion process, relative to the outcome (y) process, this is a useful feature. (An example is when we are trying to estimate treatment effects. In doing so, we can use post-treatment variables to model inclusion in the sample, and we can do so without having to worry about issues of compatibility between the inclusion model and the model we are using to quantify treatment effects. If we wanted to model outcome directly—that is, if we wanted to use an imputation strategy—we’d have to ensure compatibility and marginalize over the values of the post-treatment variable.)
When I presented this picture, it was interesting to see some people in the audience nodding their heads enthusiastically, but a few looked at me like I had two heads. Someone from the latter camp asked, why is it at all useful to be able to recover an “inaccurate” description of the relationship between the x and y variables?
This is a question about the value of an estimator’s “robustness to misspecification,” by which I mean that the estimator consistently estimates a statistic, $latex \theta$, that describes the population, but that $latex \theta$ may not, itself, be a “parameter” in a “data generating process” that gives rise to the population values. One way to look at it is to propose that outcome models are always approximations of complex, unknowable relationships, and so we are always estimating $latex \theta$-type objects rather than parameters in any actual data generating process. That being the case, we want to be sure that we are at least estimating an approximation that characterizes the population. To put it another way, the statistic, $latex \theta$, contains all the practical information that we can use, without containing all the information that may be needed to characterize the full data generating process. Moving beyond $latex \theta$ may require commitments to further modeling assumptions that we would prefer to avoid; rather, we are content with the population summary that $latex \theta$ provides, so long as we can estimate that summary consistently with our sample.
This all comes into play in a few situations. One is where the relationships between variables are highly irregular—e.g., lots of obscure nonlinearities—but there are pronounced lower-order features that explain enough variation such that a linear approximation is sufficient for the sake of making a decision. To put this more straightforwardly, we have a decision to make, and it depends simply on the general extent to which y is increasing or decreasing in x. In this case, a linear, or possibly quadratic, approximation would suffice. Another situation where this comes into play is with heterogeneous treatment effects. Suppose we want a difference in means estimate of the average treatment effect in the population, but there is substantial heterogeneity in the differences in potential outcomes. Then, a difference in means from a non-representative sample may fail to recover the population difference in means, and so we want to adjust—e.g. with weighting—to get back to the population difference in means. In my view, the two situations described in this paragraph are essentially the same, and the principles are all being illustrated in the picture above. Also, I see clear links between arguments extolling “robustness to misspecification” and the so-called “design-based” orientation toward inference that takes outcomes in the population as fixed and randomness coming from the sampling or experimental design.
